公共最长子序列

webkong 6/23/2017

适用的解往往不是最好的，但是肯定是最平衡的。

# 目录

# Diff 算法

用过版本控制的同学都见过 diff 文件，在两个不同的文件之间找差异，在删掉的地方用'-'标识，在新增加的地方用'+'标识(并不是所以的都是-+，但是都有标识新增和删掉的符号)。例如最流行的 Git 的 diff 文件(点击查看大图)：

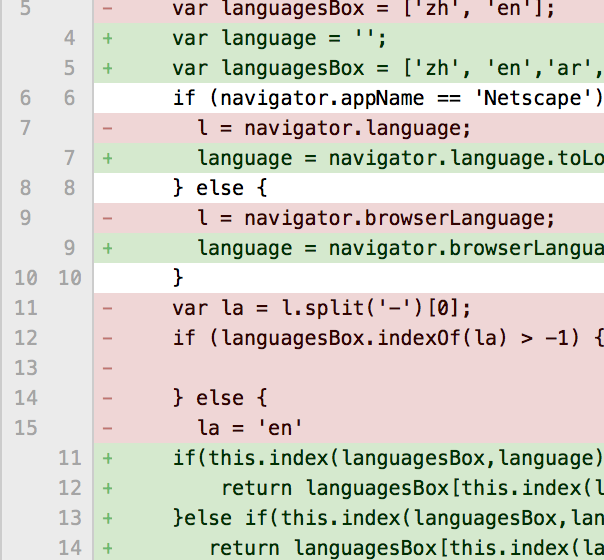
如图所示，很明确的就知道两个文件的差异是什么，本次的修改又有哪些。那么 diff 的原理又是什么呢？

# LCS

LCS (最长公共子序列, Longest common subsequence problem)。

diff 操作，就是基于解决 LCS 问题，也就是说，假设给出两个序列：

  a b c d f g h j q z   //A

  a b c d e f g i j k r x y z   //B

1
2
3

我们的目的是，在这两个序列当中，找到相同顺序的最长序列（we want to find a longest sequence of items that is present in both original sequences in the same order）。注意是相同顺序的序列而不是连续的序列。

那么对于上面的两个序列(A、B)来说，他们的最长公共子序列是：

  a b c d f g  j  z

那么， A 对于 B 序列的差异就可以表示成：

  e   h i   q   k r x y
  +   - +   -   + + + +

1
2
3

上面， +表示新增的字符， -表示要删除的字符。

也就是说，如果 A 序列要变成 B 序列，要在相应的位置上进行增加和删除操作。

当然我们在平时比较文件的 diff 时候，会把文件转化成两个列表，列表的每一个元素就是文件的某一行，所以在上面 git 的 diff 文件中会显示每一行的 - 和 + 。

用 js 简单实现一个算法：

let a1 = ["a", "b", "c", "d", "f", "g", "h", "j", "q", "z", "k"];
let b1 = ["a", "b", "c", "d", "e", "f", "g", "i", "j", "k", "r", "x", "y", "z"];

let clsQuence = [];

function lcs(a, b) {
  if (a.length > 0 && b.length > 0) {
    if (a[0] === b[0]) {
      clsQuence.push(a[0]);
      a1.shift();
      b1.shift();
    } else {
      let index = b.indexOf(a[0]);
      if (index > -1) {
        clsQuence.push(a[0]);
        a1.shift();
        b1 = b.slice(index);
      } else {
        a1.shift();
      }
    }
    lcs(a1, b1);
  } else {
    return;
  }
}
lcs(a1, b1);
console.log(clsQuence);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

# 参考

https://en.wikipedia.org/wiki/Diff_utility (opens new window)

https://en.wikipedia.org/wiki/Longest_common_subsequence_problem (opens new window)

https://en.wikipedia.org/wiki/Dynamic_programming (opens new window)

全面理解虚拟 DOM，实现虚拟 DOM (opens new window)

文档中心

Choose mode